自省 自行 自醒

深入浅出 effective_cache_size

数据库原理
Word count: 2kReading time: 9 min
2024/02/19
loading

前言

关于 effective_cache_size 参数许久之前也曾翻译过一篇文章，最近在复核 14 internal 的时候，又有了一些新的理解与感触。

何如

众所周知，在 PostgreSQL 的双缓存架构下，其对于自己的 shared_buffers 有着”绝对”掌控权，但是对于文件系统缓存一无所知，加之 cache 几乎无处不在，除了文件系统，存储有、RAID 卡有、磁盘可能也有，因此优化器还要考虑到这些缓存的存在

We also use a rough estimate “effective_cache_size” of the number of disk pages in Postgres + OS-level disk cache. (We can’t simply use NBuffers for this purpose because that would ignore the effects of the kernel’s disk cache.)

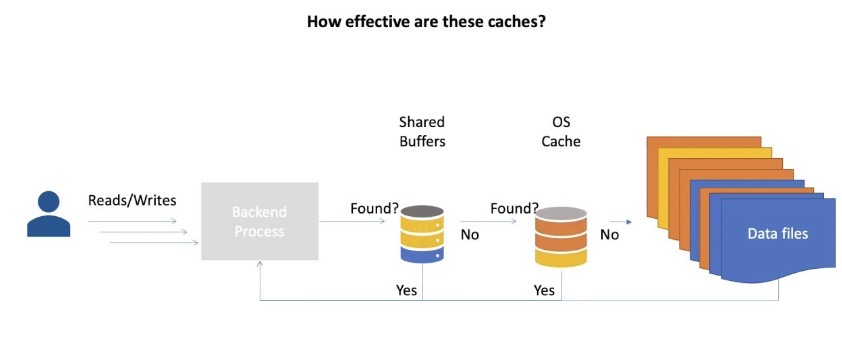
effective_cache_size 便是做这个的，简而言之，此参数用于告诉优化器有多少缓存可以用于查询，包括操作系统的缓存，按照一般经验，推荐设置为 RAM * 0.7

Sets the planner’s assumption about the effective size of the disk cache that is available to a single query.

然而官网的解释比较粗糙，其详细原理并没有过多阐述，只是给出了如何调整的建议，越高越可能使用索引，越低则倾向于使用顺序扫描。

This is factored into estimates of the cost of using an index; a higher value makes it more likely index scans will be used, a lower value makes it more likely sequential scans will be used

更高的数值会使得索引扫描更可能被使用，更低的数值会使得顺序扫描更可能被使用。

让我们看看代码中的注解，深入了解其原理。代码位于 costsize.c 中

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
/*
 * index_pages_fetched
 *	  Estimate the number of pages actually fetched after accounting for
 *	  cache effects.
 *
 * We use an approximation proposed by Mackert and Lohman, "Index Scans
 * Using a Finite LRU Buffer: A Validated I/O Model", ACM Transactions
 * on Database Systems, Vol. 14, No. 3, September 1989, Pages 401-424.
 * The Mackert and Lohman approximation is that the number of pages
 * fetched is
 *	PF =
 *		min(2TNs/(2T+Ns), T)			when T <= b
 *		2TNs/(2T+Ns)					when T > b and Ns <= 2Tb/(2T-b)
 *		b + (Ns - 2Tb/(2T-b))*(T-b)/T	when T > b and Ns > 2Tb/(2T-b)
 * where
 *		T = # pages in table
 *		N = # tuples in table
 *		s = selectivity = fraction of table to be scanned
 *		b = # buffer pages available (we include kernel space here)
 *
 * We assume that effective_cache_size is the total number of buffer pages
 * available for the whole query, and pro-rate that space across all the
 * tables in the query and the index currently under consideration.  (This
 * ignores space needed for other indexes used by the query, but since we
 * don't know which indexes will get used, we can't estimate that very well;
 * and in any case counting all the tables may well be an overestimate, since
 * depending on the join plan not all the tables may be scanned concurrently.)
 *
 * The product Ns is the number of tuples fetched; we pass in that
 * product rather than calculating it here.  "pages" is the number of pages
 * in the object under consideration (either an index or a table).
 * "index_pages" is the amount to add to the total table space, which was
 * computed for us by make_one_rel.
 *
 * Caller is expected to have ensured that tuples_fetched is greater than zero
 * and rounded to integer (see clamp_row_est).  The result will likewise be
 * greater than zero and integral.
 */
double
index_pages_fetched(double tuples_fetched, BlockNumber pages,
					double index_pages, PlannerInfo *root)
{
  ...

看起来很生硬，代码看得我云里雾里。简而言之，计算采用了 Mackert 和 Lohman 提出的模型，这个方法旨在估算有限 LRU 缓冲区下索引扫描的 I/O 成本。

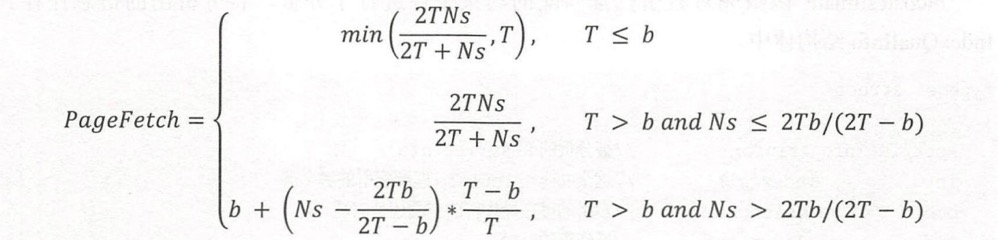
该公式基于以下参数：

  • T：表中的页面数
  • N：表中的元组数
  • s：约束条件的选择率
  • b：表上的页面已经在缓存中的数量

index_pages_fetched 通过这个公式估算，在考虑到缓存效应后，实际需要获取的页面数量。这种方法帮助优化器在考虑不同查询执行计划时，更准确地估算 I/O 成本，从而选择最佳的查询执行策略。

假设当前查询中涉及的所有表的总页面是 total_pages，effective_cache_size 表示当前查询中涉及的所有表已经加载到缓存的总页面数，那么 (细节可以参照查询优化深度探索一书)：

分析

代码过于晦涩，让我们看个实际例子：

1
2
3
4
5
6
7
8
9
10
postgres=# CREATE TABLE t_ordered AS SELECT id, ceil(random() * 100000000) AS r FROM generate_series(1, 1000000) AS id;
SELECT 1000000
postgres=# analyze t_ordered ;
ANALYZE
postgres=# select attname,correlation from pg_stats where tablename = 't_ordered';
 attname |  correlation  
---------+---------------
 id      |             1
 r       | -0.0018580947
(2 rows)

t_ordered 表的 id 列相关性为 1，表示完美关联，元组在磁盘上的物理顺序与索引中 TIDS 的逻辑顺序完美相关，那么每个页面只会被访问一次：Index Scan 节点将顺序地从一个页面跳到另一个页面，逐个读取元组。

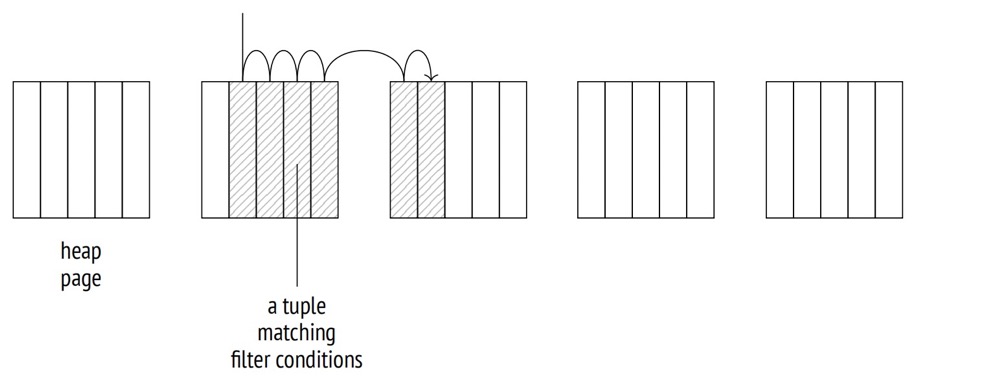
而 r 列为 0.0018，越接近 0 的值表示数据越杂乱无章，Index Scan 节点必须在页面之间跳转，而不是顺序读取；在最坏的情况下，访问的页面数量会达到获取的元组数量。

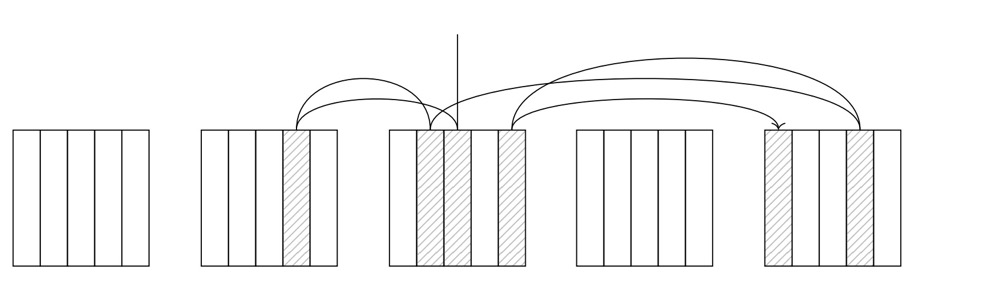
让我们粗略计算下总成本是如何计算出来的，记住前提是 id 列的相关性为 1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
postgres=# create index on t_ordered(id);
CREATE INDEX
postgres=# create index on t_ordered(r);
CREATE INDEX
postgres=# analyze t_ordered ;
ANALYZE
postgres=# set enable_bitmapscan to off;
SET
postgres=# set enable_seqscan to off;
SET
postgres=# explain select * from t_ordered where id < 100000;
                                        QUERY PLAN                                        
------------------------------------------------------------------------------------------
 Index Scan using t_ordered_id_idx on t_ordered  (cost=0.42..3351.27 rows=98677 width=12)
   Index Cond: (id < 100000)
(2 rows)

优化器预估返回 98677 条，那么选择率为 0.098677

1
2
3
4
5
postgres=# select 98677/reltuples as selectivity from pg_class where relname = 't_ordered';
 selectivity 
-------------
    0.098677
(1 row)

索引扫描的成本包括：

  1. CPU cost of searching B+-tree，扫描 B 树的成本
  2. CPU cost of scanning index tuples in leaf pages，在叶子页搜索匹配元组的成本
  3. I/O cost of leaf pages，叶子页面的 I/O 成本
  4. I/O cost of heap pages，堆页面的 I/O 成本
  5. CPU cost of scanning heap tuples，扫描堆元组的成本

具体细节可以参考 https://www.interdb.jp/pg/pgsql03/02.html，此处粗略计算一下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
postgres=# WITH costs(idx_cost, tbl_cost) AS (
  SELECT
  (
    SELECT round(
      current_setting('random_page_cost')::real * pages +
      current_setting('cpu_index_tuple_cost')::real * tuples +
      current_setting('cpu_operator_cost')::real * tuples
    )
    FROM (
      SELECT relpages * 0.098677 AS pages, reltuples * 0.098677 AS tuples
      FROM pg_class WHERE relname = 't_ordered_id_idx'
    ) c
  ),
  (
    SELECT round(
      current_setting('seq_page_cost')::real * pages +
      current_setting('cpu_tuple_cost')::real * tuples
    )
    FROM (
      SELECT relpages *0.098677 AS pages, reltuples * 0.098677 AS tuples
      FROM pg_class WHERE relname = 't_ordered'
    ) c
  )
)
SELECT idx_cost, tbl_cost, idx_cost + tbl_cost AS total
FROM costs;
 idx_cost | tbl_cost | total 
----------+----------+-------
     1824 |     1524 |  3348
(1 row)

我们计算出来的结果为 3348，和优化器算出来的 3351 接近，当然这是一个近似值。现在，让我们基于随机列的查询 (返回大致相同的行数，使选择率大致相同)：

1
2
3
4
5
6
postgres=# explain select * from t_ordered where r < 10000000;
                                        QUERY PLAN                                        
------------------------------------------------------------------------------------------
 Index Scan using t_ordered_r_idx on t_ordered  (cost=0.42..24555.56 rows=98071 width=12)
   Index Cond: (r < '10000000'::double precision)
(2 rows)

计算方式类似，不过此处是 random 列，相关性并非 1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
postgres=# WITH costs(idx_cost, tbl_cost) AS (
  SELECT
  (
    SELECT round(
      current_setting('random_page_cost')::real * pages +
      current_setting('cpu_index_tuple_cost')::real * tuples +
      current_setting('cpu_operator_cost')::real * tuples
    )
    FROM (
      SELECT relpages * 0.098071 AS pages, reltuples * 0.098071 AS tuples
      FROM pg_class WHERE relname = 't_ordered_r_idx'
    ) c
  ),
  (
    SELECT round(
      current_setting('random_page_cost')::real * tuples +
      current_setting('cpu_tuple_cost')::real * tuples
    )
    FROM (
      SELECT relpages * 0.098071 AS pages, reltuples * 0.098071 AS tuples
      FROM pg_class WHERE relname = 't_ordered'
    ) c
  )
)
SELECT idx_cost, tbl_cost, idx_cost + tbl_cost AS total
FROM costs;
 idx_cost | tbl_cost | total  
----------+----------+--------
     1812 |   393265 | 395077
(1 row)

可以看到这种方式计算出来的值和优化器算出来的相差极大，原因不难理解，优化器考虑了缓存，默认的 effective_cache_size 为 4GB。

假如我们将其设为最小值，这样计算出来的值 394988.27 就和我们计算出来的值十分接近了。

1
2
3
4
5
6
7
8
postgres=# set effective_cache_size to '8kB';
SET
postgres=# explain select * from t_ordered where r < 10000000;
                                        QUERY PLAN                                         
-------------------------------------------------------------------------------------------
 Index Scan using t_ordered_r_idx on t_ordered  (cost=0.42..394988.27 rows=98071 width=12)
   Index Cond: (r < '10000000'::double precision)
(2 rows)

小结

小结一下

  1. effective_cache_size 用于告诉优化器有多少缓存可以用于查询，并非真正分配这么多，仅仅是一个参考值，当评估叶子页面的 I/O 成本时，优化器会考虑到 effective_cache_size，越大，索引扫描的成本就越低，也就越倾向于使用索引扫描
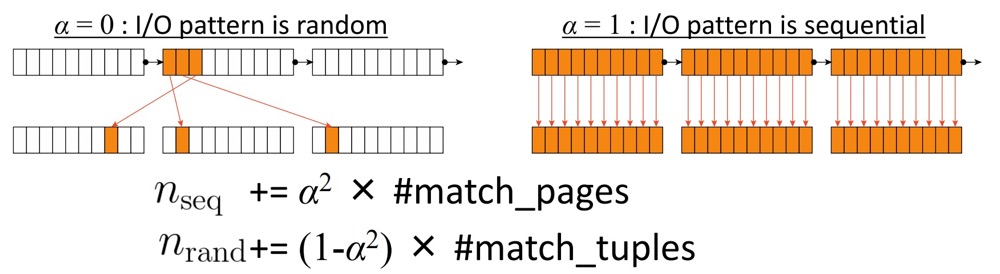
  2. 而 correlation 相关性决定了元组在磁盘上的物理顺序和逻辑顺序，也决定了堆页面的 I/O 成本，能否顺序访问的概率

参考

https://www.interdb.jp/pg/pgsql03/02.html

https://www.cybertec-postgresql.com/en/effective_cache_size-a-practical-example/

https://www.cybertec-postgresql.com/en/effective_cache_size-what-it-means-in-postgresql/

CATALOG
  1. 1. 前言
  2. 2. 何如
  3. 3. 分析
  4. 4. 小结
  5. 5. 参考
Total : 62
2025
2024
2023
2022
2021
年终总结 巡检 Greenplum SQL 优化 个人感想 流复制 新特性解读 postgres-howto 数据库原理 PostgreSQL 生态 Double Buffer 培训认证 Online DDL 书籍与资料 内存 网络 闪回 统计信息 升级 抒发情怀 权限 VACUUM 原理 锁 备份恢复 分区表